07.22.2021
Happy Pi Approximation Day
Well, basically, it's just an excuse for mathematicians – particularly faculty members in university math departments – to get together, talk trash about the Tauist splinter group (more on that later), tell obscure math jokes and eat slices of pie. Apple, in honor of Sir Isaac Newton, seems to be the flavor of choice. Also called "Casual Pi Day", the date was chosen because, in European notation, the date 22/7 is the same as 22 divided by 7, which gives an approximation of pi (the lower-case Greek letter pi). Pi is the mathematical symbol for the relationship between a circle's diameter and its circumference (expressed as C = pi times d where C is the circumference and d is the diameter) and between a circle's area and its radius (expressed as pi = A/r squared, where A is the area and r is the radius). The symbol pi, however, didn't begin to be used until the Welsh mathematician William Jones introduced it in 1706.
The earliest recorded attempt to understand how circles "work" – what the relationship is among the circumference, diameter and area – took place in Babylon (in what is modern Iraq) about 1900 BC. Their calculations were really rough, as in the number "3". You can't get more basic, or inaccurate, than that. To be fair, though, they weren't the only ones who used 3 (a passage in the Old Testament of the Bible, 1 Kings 7:23, calculates the circumference of a cast bronze circle using that ratio). Also, a slightly later Babylonian tablet did refine the ratio to 3.125. An Egyptian papyrus scroll dated to 1650 BC gave an approximate value of 3.1605, which isn't bad. In China, the mathematician Zu Chongzhi (429-501 AD) came up with the fraction 355/113 as his closest approximation. This can be expressed as 3.1415929, which is accurate out to six of the seven digits past the decimal.
But pi, even though it wasn't called that yet, really got its start in ancient Greece. Archimedes of Syracuse (287-212 BC) decided to take a circle and draw a polygon that inscribed it (that is, where the corners of the figure just touched the inside of the circle) and another that circumscribed it (the lines of the polygon just touched the outside of the circle). By calculating the perimeter of the two polygons (dividing up each figure into right triangles and using the Pythagorean Theorem to determine the length of the outer side), he estimated circumference as being between those two limits. Assigning the symbols Pn for the perimeter of the inscribed circle and Pn for the circumscribed perimeter, where "n" is the number of sides of the polygon, pi can be approximated as Pn lesser/equal to pi lesser/equal to Pn. Archimedes eventually came up with the approximation 223/81 less than pi less than 22/7. The more sides he used on the two polygons, the more accurate that approximation. The best estimate of the average of these two bounds is 3.1418, which is actually not as accurate as the estimate made by Zu Chongzhi.
Since there is no limit to the number of sides that a polygon can have, the estimate can get closer and closer to the actual value of the circumference of a circle without actually reaching the true, complete value. It has been determined that pi is an irrational number, meaning that it is infinite and, in decimal notation, does not have a repeated pattern of numbers. By using formulae to calculate an infinite series, Febrice Bellard, a French computer programmer, calculated pi to 2,699,999,990,000 (that is nearly 2,700 billion) places to the right of the decimal place.
Oh, and the Tauists mentioned before? It seems that not everyone celebrates Pi Approximation Day, or even accepts the purity of pi. In 2010, physicist Michael Hartl published a paper "The Tau Manifesto", which presents the heretical view that "Pi is Wrong!" Instead of using pi, the ratio of the circumference of a circle to its diameter, he proposed using a ratio of the circumference to the circle's radius, which he claims is more accurate than pi. He suggested using the Greek letter tau, which equals 2pi. Pi purists, of course, reject such an idea, cast Dr. Hartl's theory into the outer darkness and go about the more serious business of eating apple pie.
So, Happy 3.142857 Day! |
 GoodCalculators.com
A collection of really good online calculators for use in every day domestic and commercial use!
GoodCalculators.com
A collection of really good online calculators for use in every day domestic and commercial use!
- Salary & Income Tax Calculators
- Mortgage Calculators
- Retirement Calculators
- Depreciation Calculators
- Statistics and Analysis Calculators
- Date and Time Calculators
- Contractor Calculators
- Budget & Savings Calculators
- Loan Calculators
- Forex Calculators
- Real Function Calculators
- Engineering Calculators
- Tax Calculators
- Volume Calculators
- 2D Shape Calculators
- 3D Shape Calculators
- Logistics Calculators
- HRM Calculators
- Sales & Investments Calculators
- Grade & GPA Calculators
- Conversion Calculators
- Ratio Calculators
- Sports & Health Calculators
- Other Calculators
 July 22nd is "Pi Approximation Day", when all fans of circles, disks and round things in general can celebrate the ratio of the diameter of a circle to its circumference. Sort of. More or less.
July 22nd is "Pi Approximation Day", when all fans of circles, disks and round things in general can celebrate the ratio of the diameter of a circle to its circumference. Sort of. More or less.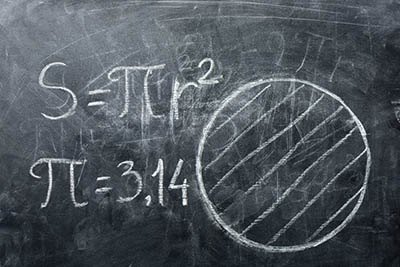 On the other hand, the approximation 22/7 is not irrational, although it is infinite. Expressed in decimal notation, it is 3.142857142857142857… which, as you can see, repeats the same six digits to the right of the decimal over and over. Compared to the actual value of pi, 3.1415926535… , 22/7 is only accurate to two digits past the decimal. That's good enough for rough calculations, and certainly good enough when slicing up an apple pie.
On the other hand, the approximation 22/7 is not irrational, although it is infinite. Expressed in decimal notation, it is 3.142857142857142857… which, as you can see, repeats the same six digits to the right of the decimal over and over. Compared to the actual value of pi, 3.1415926535… , 22/7 is only accurate to two digits past the decimal. That's good enough for rough calculations, and certainly good enough when slicing up an apple pie.