Silver Ratio Calculator

You can use this Silver Ratio Calculator to quickly and easily use the Silver Ratio to identify a missing value.

How to use the calculator:

1. Input either the width (A) or the length (B).
2. Click on the "Calculate" button to compute the missing value.

Reference

The silver ratio, which is typically represented by δ_s, operates in a similar manner to the renowned golden ratio, and it is used in a variety of geometric and mathematical expressions.

The aspect ratio of a silver rectangle is 1:1+√2, or roughly 1:2.41421356.

The following continued fraction converges to δ_s:

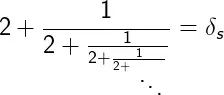
It is possible to resolve this arithmetic expression by solving the following equation: x = 2 + 1/x

Furthermore, the silver ratio appears as the limiting ratio of the solutions to the Pell equation: 2x² ± 1 = y²

For example, the first few solution pairs are as follows:

(1, 1)   2x² − 1 = y²

(2, 3)   2x² + 1 = y²

(5, 7)   2x² − 1 = y²

(12, 17)   2x² + 1 = y²

(29, 41)   2x² − 1 = y²

(70, 99)   2x² + 1 = y²

(169, 239)   2x² − 1 = y²

(408, 577)   2x² + 1 = y²

(985, 1393)   2x² − 1 = y²

(2378, 3363)   2x² + 1 = y²

...

If you apply the ratio of the consecutive y terms, you have the following:

3/1 = 3

7/3 = 2.333333

17/7 = 2.428571

41/17 = 2.411765

99/41 = 2.414634

577/239 = 2.414225

3363/1393 = 2.414213

As the above reveals, the ratio converges to 1+√2. A similar pattern will emerge if you apply the ratio of the sequential x terms.

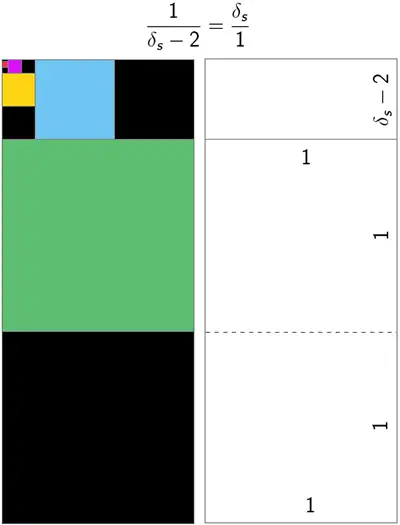
To comprehend δ_s from a geometric perspective, let's say you have a rectangle of which the sides are in a ratio of 1:δ_s. When you remove two perfect squares from the rectangle, the remaining rectangle is referred to as a silver rectangle. Repeating the process will result in the following pattern:

You may also be interested in our Ratio Calculator or Aspect Ratio Calculator