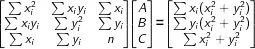Least-Squares Circle Calculator

You can use this least-squares circle calculator to identify the circle that fits the provided points in the plane most effectively from the least-squares perspective.

You can use this calculator in two simple steps:

1. Input the X and Y data pairs in the fields provided.
2. Click on the "Calculate" button, and the calculator will determine the coordinates of the radius and center of the circle.

Understanding the Best Fit Circle

In a situation in which you have the data points x, y that are distributed in a ring-shape on an x-y plane, the least-squares regression can be used to determine the equation of a circle that will best fit with the available data points; i.e., the following regression will help you to calculate the k, m, and r values of the curve:

(x − k)² + (y − m)² = r²

When you use the least-squares, you determine the "best fit" by minimizing the equation as follows:

F(k, m, r) = ∑[(x_i − k)² + (y_i − m)² − r²]²

The equation of the circle is linearized by the model ∂F/∂k = 0, ∂F/∂m = 0, and ∂F/∂r = 0. As such, we have the following:

(x − k)² + (y − m)² = r²

x² − 2kx + k² + y² − 2my + m² = r²

x² + y² = 2kx + 2my + r² − k² − m²

x² + y² = Ax + By + C

This results in a linear equation with the coefficients A, B, and C undetermined. As such, you can use the matrices to solve the least-squares problem. Once you have determined A, B, and C, it is possible to work backward to compute k, m, and r.

Finding A, B, and C with Matrices

The circle regression model is supported by the following matrix equation:

where n is the number of data points (x_i, y_i).

In a situation in which the 3-by-3 matrix outlined on the left is invertible, the A, B, and C values are unique, and this determines the best fit circle.

You can use the A, B, and C values to subsequently determine k, m, and r:

k = A/2

m = B/2

r = (√4C + A² + B²)/2

Example:

Let's say we want to identify the equation of the circle that best fits the following four data points: (0, 1), (2, 5), (1, 6), and (7, 6).

The use of the matrix equation or the least squares circle calculator results in the following:

(x − 4.2408)² + (y − 2.4630)² = 4.3220².

You may also be interested in our Quadratic Regression Calculator or Linear Regression Calculator